Ohmsches Gesetz für eine vollständige Kette und für einen Abschnitt einer Kette: Möglichkeiten zum Schreiben der Formel, Beschreibung und Erklärung
Für einen professionellen Elektriker oder Elektronikspezialisten gibt es keine Möglichkeit, das Ohmsche Gesetz bei seiner eigenen Tätigkeit zu umgehen und Probleme im Zusammenhang mit der Einrichtung, Einstellung und Reparatur elektronischer und elektrischer Schaltkreise zu lösen.
Eigentlich muss jeder dieses Gesetz verstehen. Denn jeder muss sich im Alltag mit Strom auseinandersetzen.
Und obwohl das Ohmsche Gesetz des deutschen Physikers im Lehrplan der weiterführenden Schulen vorgesehen ist, wird es in der Praxis nicht immer rechtzeitig studiert. Daher werden wir in unserem Material ein so relevantes Thema für das Leben betrachten und die Möglichkeiten zum Schreiben der Formel verstehen.
Der Inhalt des Artikels:
Einzelner Abschnitt und vollständiger Stromkreis
Betrachtet man einen Stromkreis unter dem Gesichtspunkt der Anwendung des Ohmschen Gesetzes auf einen Stromkreis, sind zwei mögliche Berechnungsmöglichkeiten zu beachten: für einen separaten Abschnitt und für einen vollwertigen Stromkreis.
Berechnung des Stroms eines Stromkreisabschnitts
Als Abschnitt eines Stromkreises wird in der Regel der Teil des Stromkreises angesehen, der die EMF-Quelle ausschließt, da er einen zusätzlichen Innenwiderstand aufweist.
Daher sieht die Berechnungsformel in diesem Fall einfach aus:
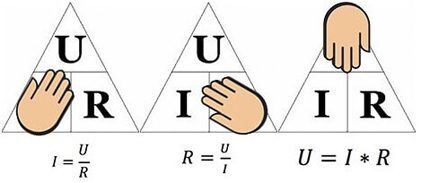
I = U/R,
Wo jeweils:
- ICH – aktuelle Stärke;
- U – angelegte Spannung;
- R - Widerstand.
Die Interpretation der Formel ist einfach: Der durch einen bestimmten Abschnitt des Stromkreises fließende Strom ist proportional zur daran angelegten Spannung und der Widerstand ist umgekehrt proportional.
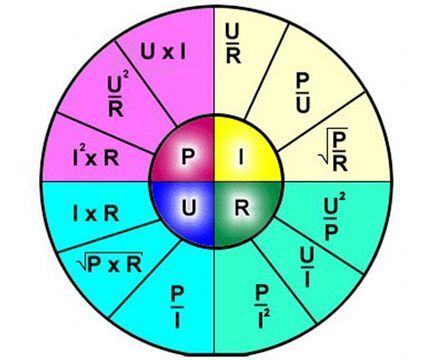
Somit beschreibt die Formel eindeutig die Abhängigkeit des Stromflusses durch einen separaten Abschnitt des Stromkreises von bestimmten Spannungs- und Widerstandswerten.
Die Formel lässt sich beispielsweise bequem verwenden, wenn die Parameter des Widerstands berechnet werden, der in den Stromkreis eingelötet werden muss, wenn Spannung und Strom angegeben sind.
Die obige Abbildung hilft beispielsweise bei der Bestimmung des Stroms, der durch einen 10-Ohm-Widerstand fließt, an den eine Spannung von 12 Volt angelegt wird. Wenn wir die Werte ersetzen, finden wir – I = 12 / 10 = 1,2 Ampere.
Die Probleme, den Widerstand (wenn Strom und Spannung bekannt sind) oder die Spannung (wenn Spannung und Strom bekannt sind) zu finden, werden auf ähnliche Weise gelöst.
So können Sie immer die benötigte Betriebsspannung, die benötigte Stromstärke und das optimale Widerstandselement auswählen.
Übrigens sind die Verbindungsdrähte eines jeden Stromkreises Widerstände. Die Belastung, die sie tragen müssen, wird durch die Spannung bestimmt.
Somit ist es wiederum mithilfe des Ohmschen Gesetzes möglich, den erforderlichen Leiterquerschnitt abhängig vom Kernmaterial genau auszuwählen.
Eine ausführliche Anleitung finden Sie auf unserer Website Berechnung des Kabelquerschnitts in Bezug auf Leistung und Strom.
Berechnungsmöglichkeit für eine komplette Kette
Ein vollständiger Stromkreis besteht aus einem Abschnitt (Abschnitten) sowie einer EMF-Quelle. Das heißt, der Innenwiderstand der EMF-Quelle wird zur vorhandenen Widerstandskomponente des Schaltungsabschnitts addiert.
Daher ist es logisch, die obige Formel leicht zu ändern:
I = U / (R + r)
Natürlich kann der Wert des Innenwiderstands der EMF im Ohmschen Gesetz für einen kompletten Stromkreis als vernachlässigbar angesehen werden, obwohl dieser Widerstandswert weitgehend von der Struktur der EMF-Quelle abhängt.
Bei der Berechnung komplexer elektronischer Schaltkreise, Stromkreise mit vielen Leitern, ist jedoch das Vorhandensein zusätzlicher Widerstände ein wichtiger Faktor.
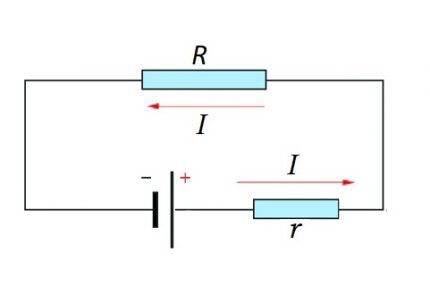
Sowohl für einen Abschnitt eines Stromkreises als auch für einen gesamten Stromkreis sollte das natürliche Moment berücksichtigt werden – die Verwendung von konstantem oder variablem Strom.
Betrachtet man die oben genannten Punkte, die für das Ohmsche Gesetz charakteristisch sind, unter dem Gesichtspunkt der Verwendung von Gleichstrom, so sieht bei Wechselstrom alles etwas anders aus.
Betrachtung der Wirkung des Gesetzes auf eine variable Größe
Das Konzept des „Widerstands“ gegenüber den Bedingungen des Wechselstromdurchgangs sollte eher als das Konzept der „Impedanz“ betrachtet werden. Dies bezieht sich auf die Kombination einer ohmschen Last (Ra) und einer reaktiven Widerstandslast (Rr).
Solche Phänomene werden durch die Parameter induktiver Elemente und die Schaltgesetze in Bezug auf einen variablen Spannungswert – einen sinusförmigen Stromwert – verursacht.
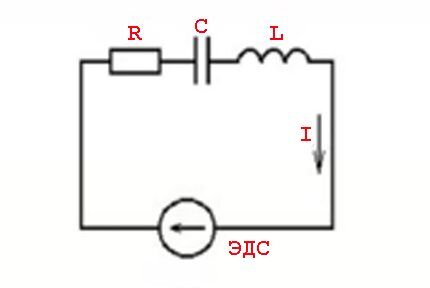
Mit anderen Worten, es gibt einen Effekt, bei dem die Stromwerte gegenüber den Spannungswerten voreilen (nacheilen), was mit dem Auftreten von Wirk- (Widerstands-) und Blindleistungen (induktiv oder kapazitiv) einhergeht.
Solche Phänomene werden nach folgender Formel berechnet:
Z=U/I oder Z = R + J * (XL -XC)
Wo: Z - Impedanz; R – aktive Last; XL , XC – induktive und kapazitive Last; J - Koeffizient.
Serielle und parallele Verbindung von Elementen
Für Elemente eines Stromkreises (Abschnitt eines Stromkreises) ist ein charakteristischer Punkt eine Reihen- oder Parallelschaltung.
Dementsprechend geht mit jeder Verbindungsart ein anderes Muster des Stromflusses und der Spannungsversorgung einher.Dabei wird das Ohmsche Gesetz je nach Möglichkeit der Einbeziehung von Elementen auch unterschiedlich angewendet.
Schaltung aus in Reihe geschalteten Widerstandselementen
Bezogen auf eine Reihenschaltung (ein Stromkreisabschnitt mit zwei Komponenten) wird folgende Formulierung verwendet:
- Ich = Ich1 =Ich2 ;
- U = U1 +U2 ;
- R = R1 + R2
Diese Formulierung zeigt deutlich, dass sich der Wert des durch einen Abschnitt des Stromkreises fließenden Stroms unabhängig von der Anzahl der in Reihe geschalteten Widerstandskomponenten nicht ändert.
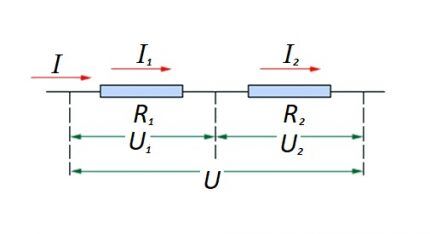
Die Größe der an die effektiven Widerstandskomponenten des Stromkreises angelegten Spannung ist die Summe und ergibt den Wert der EMK-Quelle.
In diesem Fall beträgt die Spannung an jeder einzelnen Komponente: Ux = I * Rx.
Der Gesamtwiderstand sollte als Summe der Werte aller Widerstandskomponenten im Stromkreis betrachtet werden.
Schaltung parallel geschalteter Widerstandselemente
Im Falle einer Parallelschaltung von Widerstandskomponenten gilt in Bezug auf das Gesetz des deutschen Physikers Ohm folgende Formulierung als gerechtfertigt:
- Ich = Ich1 +Ich2 … ;
- U = U1 =U2 … ;
- 1/R = 1/R1 + 1/R2 + …
Möglichkeiten zur Erstellung von Schaltungsabschnitten „gemischter“ Art bei Verwendung paralleler und serieller Verbindungen sind nicht ausgeschlossen.
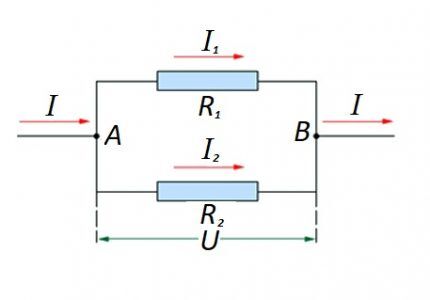
Bei solchen Optionen erfolgt die Berechnung üblicherweise dadurch, dass zunächst der Widerstandswert der Parallelschaltung berechnet wird. Anschließend wird der Wert des in Reihe geschalteten Widerstands zum erhaltenen Ergebnis addiert.
Integrale und differenzielle Rechtsformen
Alle oben genannten Punkte mit Berechnungen gelten für Bedingungen, bei denen in Stromkreisen Leiter mit sozusagen „homogener“ Struktur verwendet werden.
Mittlerweile hat man es in der Praxis häufig mit der Erstellung von Schaltplänen zu tun, bei denen sich die Struktur der Leiter in verschiedenen Abschnitten ändert. Beispielsweise werden Drähte mit größerem oder umgekehrt kleinerem Querschnitt aus unterschiedlichen Materialien verwendet.
Um solchen Unterschieden Rechnung zu tragen, gibt es eine Variante des sogenannten „differential-integralen Ohmschen Gesetzes“. Für einen infinitesimalen Leiter wird die Stromdichte in Abhängigkeit vom Spannungs- und Leitfähigkeitswert berechnet.
Für die Differenzrechnung wird folgende Formel verwendet: J = ό * E
Für die Integralrechnung lautet die Formulierung dementsprechend: I * R = φ1 – φ2 + έ
Allerdings stehen diese Beispiele eher in der Schule der höheren Mathematik und werden in der realen Praxis eines einfachen Elektrikers nicht wirklich verwendet.
Schlussfolgerungen und nützliches Video zum Thema
Eine detaillierte Analyse des Ohmschen Gesetzes im Video unten wird dazu beitragen, das Wissen in dieser Richtung endgültig zu festigen.
Eine einzigartige Videolektion stärkt qualitativ die theoretische schriftliche Präsentation:
Die Arbeit eines Elektrikers oder die Tätigkeit eines Elektronikingenieurs ist untrennbar mit Momenten verbunden, in denen man das Gesetz von Georg Ohm tatsächlich in Aktion beobachten muss. Dies sind Binsenweisheiten, die jeder Fachmann kennen sollte.
Umfangreiche Kenntnisse zu diesem Thema sind nicht erforderlich – es reicht aus, die drei Hauptvarianten des Wortlauts zu erlernen, um ihn erfolgreich in der Praxis anzuwenden.
Möchten Sie das obige Material durch wertvolle Kommentare ergänzen oder Ihre Meinung äußern? Bitte schreiben Sie Kommentare in den Block unter dem Artikel. Wenn Sie Fragen haben, zögern Sie nicht, unsere Experten zu fragen.



